Геометрическая оптика

          Мы видели, что распространение света – волновой процесс. С помощью волновой теории мы можем решать задачи распространения света как в однородной среде, так и через любую оптическую систему. Однако в очень многих случаях (формирование светового пучка, получение изображений и пр.) решение можно получить более простым путем с помощью геометрической оптики.

          Геометрическая оптика использует представление о световых лучах – математических линиях, вдоль которых происходит распространение энергии световых волн. Модель луча можно получить ставя после источника света ряд диафрагм с малыми круглыми отверстиями. В результате получим узкий световой пучок. В пределе, при уменьшении диаметра отверстий, можно, казалось бы, получить бесконечно узкий пучек – световой луч. Но благодаря дифракции реальный пучок расширяется. Как мы видели, угол дифракционной расходимости лучей порядка , таким образом, только в предельном случае, когда  дифракции нет и можно было бы говорить о луче как о геометрической линии, направление которой определяет направление распространения световой энергии. Таким образом, световой луч есть абстрактное математическое понятие, а не реальный физический образ, и геомтрическая оптика есть лишь предельный случай  волновой оптики, соответствующий .

          В основе геометрической оптики лежит принцип Ферма из которого следуют законы распространения световых лучей, установленные ранее опытным путем. Это

1.     Закон прямолинейного распространения света в однородной среде

2.     Закон отражения

3.     Закон преломления

Кроме  того, действует Принцип обратимости и закон независимости световых пучков.

Большинство расчетов оптических приборов (получение изображения объекта, увеличение, яркость и т.п.) базируется на этих законах Однако для понимания более тонких явлений (например, разрешающей способности) представлений геоиетрической оптики недостаточно и нужно учитывать волновую природу света .

Принцип Ферма.

              В оптически однородном веществе свет распространяется прямолинейно, но на границах раздела сред – отражается и преломляется и его путь становится ломаным. В неоднородной среде,  где показатель преломления непрерывно меняется, лучи света являются кривыми линиями. Если не рассматривать дифракцию, то распространение светового луча описывается общим принципом, носящим название принцип Ферма. Сам Ферма сформулировал свой принцип в 1679 году так. Свет при распространении от одной точки к другой выбирает путь, которому соответствует наименьшее время распространения.

          При этом Ферма руководствовался теологическими соображениями: природа действует целенаправленно; она не может быть расточительной и должна достигать своих целей с наименьшей затратой средств.. Эти соображения, конечно, не могут служить объяснением, но сам принцип в основнои верен, требует только некоторых уточнений.

          Выразим принцип Ферма количественно. Для этого введем оптическую длину пути l=ns,  а в случае неоднородной среды –  dl=nds, где s – геометрический путь луча, ds – его малый отрезок, n – показатель преломления среды. Таким образом, оптическая длина пути из точки А в точку В выражается криволинейным интегралом 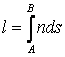. Свет распространяется по пути, оптическая длина которого экстремальна, т.е. она является либо минимальной из всех возможных, либо максимальной, либо стационарной. Условие экстремальности сводится к требованию, чтобы вариация этого интеграла равнялась нулю: . Это и есть математическая формулировка принципа Ферма.

Принцип Ферма может быть получен из волновой оптики (там речь идет о нормалях к фронту волны) и может быть строго доказан. Из принципа Ферма следуют все три закона геоиетрической оптики для распространения света. Также из него следует закон обратимости: если свет распространяется из А в В по некоторому пути, то из В в А он будет распространяться по тому же пути.

          Рассмотрим некоторые частные случаи.

1)     Прямолинейное распространение света в однородной среде – очевидно.

2)     Отражение от плоской поверхности

 

В’

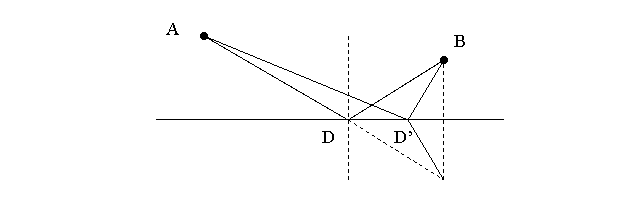Доказательство видно из чертежа: Путь AD+DB=AD+DB’ Путь AD’+D’B=AD’+D’B’. Но длина ADB’  меньше, чем AD’B.

3)Преломление на плоской поверхности раздела двух сред. Точно так же, если полсчитать путь преломленного луча и найти его минимум, получим закон преломления.

4) Пример стационарности хода луча – прохождение лучей через линзу. Лучи прохолят так, что все пути лучей таутохронны –  там, где линза тоньше геометрический путь длиннее.

5) Миражи.

          Если смотреть летом вдоль раскаленного шоссе, то где-то далеко асфальт кажется мокрым, покрытым лужами. Причина этой иллюзии в том, что у разогретого асфальта выше температура воздуха , а давление воздуха  одинаковое: , следовательно, у разогретого асфальта меньше плотность воздуха и концентрация его молекул .   Меньшая концентрация молекул означает, меньшее значение показателя преломления, так как при небольшой плотности из формулы Лоренц-Лорентца следует . Свет поворачивает в оптически более плотную среду:

          При скользящем падении света свет от лужи хорошо отражается. В этой луже, которой на самом деле нет, видны отражения неба, солнца или деревьев.

          Эти отражения и есть миражи. Они особенно хорошо видны в пустыне.

 

Оптическая система.

Под оптической системой понимают систему линз, зеркал, призм и т.п., служащую для изменения направления световых лучей. Оптическая система используется для различных целей. Она может дополнять глаз при рассматривании изображение объекта на экране; она позволяет  сконцентрировать световую энергию на малом участке  поверхности или создать параллельный пучек лучей и т.д. Во всех случаях роль оптической системы сводится к изменению телесных углов, в пределах которых распространяются лучм, исходящие от объекта.

Большинство оптических систем состоит из сферических поверхностей, разделяющих однородные среды с различными показателями преломления. Если центры кривизны всех поверхностей лежат на одной прямой системаназывается  центрированной. Прямая, на которой лежат все центры кривизны, является осью симметриии и называется  оптической осью системы.

При расчете оптических систем пучки света рассматриваются как совокупности бесконечного числа лучей, удовлетворяющих законам прямолинейного распространения в однородной среде, отражения и преломления на границе двух сред. Размеры элементов оптических систем (зеркал, линз, диафрагм и т.п.) как правило значительно (на несколько порядков) больше длины световой волны, поэтому геометрическая оптика оказывается хорошим приближением при описании оптических систем и позволяет простыми средствами решать широкий круг задач, связанных с образованием изображения, его освещенностью и т.п. Однако для решения более тонких вопросов, таких, как, например, разрешающая способность оптических инструментов требуется выход за рамки этого приближения и учет волновой природы света, которая проявляется в явлениях дифракции. Дифракция накладывает принципиальное ограничение на качество изображения –  вместо точечного изображения точки получается дифракционная картина в виде концентрических темных и светлых колец, и изображение объекта размывается. В высококачественных приборах именно это ограничение преимущественно определяет разрешающую способность прибора.

Оптическое изображение.

Представим себе пучек лучей такой, что все лучи нормальны к некоторой сферической поверхности. Такой пучек называется гомоцентрическим, а точка пересечения лучей называется их фокусом. (Частный случай – пучек параллельных лучей).

Оптическое изображение – это картина, получаемая в результате прохождения через оптическую систему лучей, распространяющихся от объекта, и воспроизводящая его контуры и детали.

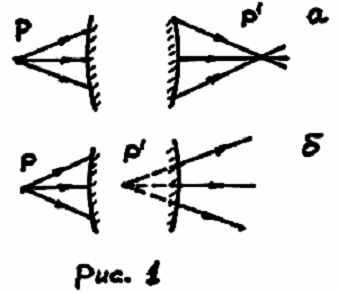
Каждой  точке  P светящегося объекта   можно сопоставить  расходящийся гомоцентрический пучек лучей (рис.1). Если после всех преломлений и отражений в оптической системе лучи пересекутся в одной точке P' , то она будет  изображением точки P. Практически лучи не сходятся строго в одной точке, а лишь в некоторой малой области вокруг неё. Если лучи сходятся в точке (по крайнкй мере в достаточном приближении), то пучек получается гомоцентрическим, а изображение называется стигматическим.

Изображения делят на действительные и  мнимые. Действительное  изображение образуется сходящимся пучком лучей (рис.1а) так, что если в месте их пересечения поставить экран, мы действительно можем увидеть изображение. Мнимое изображение получается, если из оптической системы выходит расходящийся пучек лучей (рис 1б), и пересекаются не сами лучи, а их продолжения, проведенные в на правлении,  противоположном направлению распространения света. Мнимое изображение нельзя непосредственно получить на экране, но оно может служить объектом для другой оптической системы. Например, мнимое изображение, полученное в плоском зеркале, служит объектом для оптической системы глаза, которая образует действительное изображение на сетчатке.

В геометрической оптике действует  принцип обратимости: если источник света поместить в точку P', то форма всех лучей останется без изменения, а их направление изменится на противоположное, и изображение окажется в точке P. Точки P и P’ называются сопряженными точками. Соответственные лучи и пучки также называются сопряженными.

Идеальная оптическая система.

Важнейшее назначение оптической системы –  давать правильное изображение объекта, который в простейшем случае представляет собой плоскую картину, расположенную перпендикулярно оптической оси. С этой точки зрения идеальная оптическая система – такая, которая дает стигматическое  изображение любой точки объекта, а изображение объекта геометрически подобно ему и расположено в плоскости, перпендикулярной оптической оси (если так расположен объект).

Реальная оптическая система всегда вносит искажения (аберрации) в изображение (исключением является изображение в плоском зеркале). Чтобы все же получить достаточно хорошее изображение, систему приходится усложнять, вводя вместо одной несколько линз, рассчитанных так, чтобы искажения, вносимые разными линзами, взаимно компенсировались, по крайней мере, в той области, которая является рабочей для данной системы. При этом, конечно, система усложняется, и расчет ее становится весьма сложной задачей. И даже идеальная с точки зрения геометрической оптики система, в которой устранены все аберрации, не может дать идеального изображения из-за дифракции. Таким образом, реальная оптическая система всегда более или менее отличается от идеальной.

Центрированная оптическая система является хорошим приближением к идеальной. Расчет ее становится особенно простым, если рассматривать только  параксиальные лучи, т.е. такие, которые составляют с оптической осью углы столь малые, что синус и тангенс угла можно приравнять самому углу (конечно, при этом нужно  чтобы показатели преломления всех сред, через которые проходят лучи, не зависели от длины волны в той области спектра, которая используется при формировании изображения). Образование изображений параксиальными лучами было впервые систематически исследовано Гауссом в 1841г., поэтому теорию идеальных центрированных оптических систем обычно называют гауссовой оптикой.

В дальнейшем мы будем рассматривать только центрированные оптические системы и параксиальные лучи.

Матрицы преобразования лучей

Преобразование луча в оптической системе удобно описывать с помощью специальных матриц.

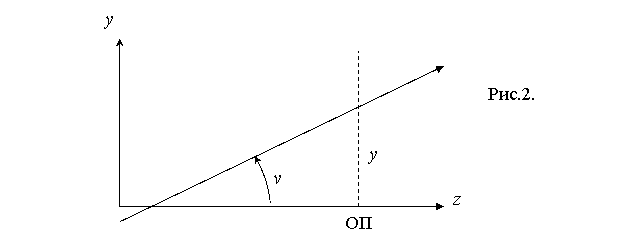
Введем общепринятую в современной оптике систему декартовых координат (Рис.2 ): ось Oz, совпадающую с оптической осью системы, а также с главным направлением, вдоль которого распространяются лучи света, направим слева направо; ось Oy будем считать расположенной в плоскости страницы и направленной вверх, а ось Ox – перпендикулярной этой плоскости и направленной от читателя. Мы будем рассматривать только меридианальные лучи, лежащие в плоскости yz  в непосредственной близости к оси Oz.

Выберем заранее любую плоскость z=const, перпендикулярную оси Oz, и назовем ее опорной плоскостью, ОП. Тогда луч можно определить по отношению к опорной плоскости двумя параметрами: высотой y, на которой этот  луч пересекает опорную плоскость, и углом v, который он составляет с осью Oz. Параметр y считается положительным, если луч пересекает опорную плоскость выше оси z и отрицательным – если ниже. Угол v измеряется в радианах и считается положительным, если он соответствует вращению против часовой стрелки от положительного направления оси z к направлению, в котором свет распространяется вдоль луча. Для проведения расчетов более удобно вместо угла  v ввести параметр V=nv, где n – показатель преломления среды, в которой распространяется луч. (Этот параметр в некоторых книгах называется «оптический направляющий косинус», но название неудачное. И мы его употреблять не будем). Любые расстояния, отмеряемые в горизонтальном направлении, тоже считаются величинами алгебраическими. Расстояние положительно, если оно отмеряется слева направо, т.е. в положительном направлении оси z, и отрицательно – в противоположном случае. В дальнейшем мы всегда будем указывать начальную и конечную точки

любого отрезка, так что слова «расстояние AB» означают, что AB положительно, если точка B лежит правее, чем A, и отрицательно – если левее. Точно так же, если сказано, например, что «AB=-6см», это означает, что отрезок AB должен быть отложен от точки A влево.

Траектория луча, поскольку он проходит через различные преломляющие поверхности системы, будет состоять из последовательных отрезков прямых линий. На каждом этапе мы должны определить параметры луча. При этом удобно на каждом этапе расчета выбирать новую ОП .

Пусть, например, мы знаем характеристики луча в какой-то точке. Это значит, что мы знаем его параметры y и  V относительно опорной плоскости, проходящей через эту точку. И пусть мы хотим определить, как пройдет луч  в другой точке (например, после того, как он прошел через линзу). Для этого проводим опорную плоскость через эту, вторую, точку и определяем параметры луча относительно второй опорной плоскости.

В дальнейшем мы увидим, что преобразование параметров y  и V луча при переходе от одной опорной плоскости, , к  другой, , будет линейным, т.е. для  любой пары опорных плоскостей оно имеет вид

Это преобразование можно записать в матричной форме:

или

,

где  – матрица преобразования, а 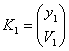  и  –  векторы луча до и после преобразования.

Для данной пары плоскостей ОП и ОП преобразование параметров любого параксиального луча описывается одной и той же матрицей, сопоставляемой промежутку между ОП и ОП. Элементы этой матрицы A,B,C и D  зависят от свойств промежутка, т.е. от того, какие преломляющие поверхности и какие среды находятся между ОП и ОП.

Для расчета хода лучей в любой системе достаточно рассмотреть только два основных процесса:

1)  Перемещение между двумя преломляющими поверхностями.

На таком участке пути луч просто проходит по прямой линии

от одной преломляющей поверхности к другой. Область между поверхностями  – оптический промежуток –  характеризуется его толщиной t и показателем преломления n среды, через которую проходит луч.

2)   Преломление на граничной поверхности между двумя областями с различными показателями преломления. Для того, чтобы определить величину отклонения прошедшего луча, необходимо знать радиус кривизны преломляющей поверхности и показатели преломления граничащих сред. (Частным случаем преломления чвляется отражение луча, см дальше).

Матрица перемещения.

 Пусть две опорные плоскости ОП и ОП ограничивают пространство с   показателем преломления n, а расстояние между ними равно t (рис.3). (Для ясности на рисунке углы даны в увеличенном масштабе; в действительности  максимальное  значение величины v для  параксиальных лучей не должно превышать 0,1 радиан (или 6 градусов). При этом погрешность вычислений в приближении параксиальной оптики оказывается менее 1%). Из рисунка видно:

 

Здесь мы учли, что. . Перейдя от угла v к параметру V и введя приведенную толщину оптического промежутка T=t/n, получим

или в матричной форме

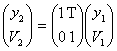
Таким образом, преобразование параметров луча описывается матрицей

                                                                           (3)

в которую в качестве матричного элемента входит приведенное расстояние T. Эта матрица называется  матрицей перемещения.  Определитель этой матрицы всегда равен единице.

Матрица преломления.

Пусть две области с показателями преломления  среды    и  разделены поверхностью с радиусом кривизны  r  (рис. 4). Чтобы одни и те же формулы были справедливы и для выпуклой, и для вогнутой поверхности радиус r считают положительным, если центр кривизны расположен справа от поверхности, и отрицательным, если он лежит слева. На рис.4  изображена поверхность положительной кривизны.

 

 

 

 

 

 

 

 

Рассмотрим луч, падающий на преломляющую поверхность. Выберем две опорные плоскости в непосредственной близости к поверхности. Первая из них, ОП, проходит через точку пересечения преломляющей поверхности и оси системы, вторая, ОП– через точку пересечения поверхности рассматриваемым лучем. Пусть на ОП параметры  луча и . Расстояние между опорными плоскостями   в   параксиальном  приближении пренебрежимо мало, следовательно . Согласно закону  преломления   или, в параксиальном приближении, . По теореме    о внешнем угле треугольника

Умножая первое из этих равенств на , а второе – на  и применяя закон преломления получим     или   

Таким образом     .

Окончательно получаем формулу для преобразования луча в виде

 

и матрица преломления имеет вид

                                                                         (3)

где    – оптическая сила поверхности.

На нашем рисунке  и все величины являются положительными. Однако матрица R  правильно описывает преломление луча и в других случаях, например, если изменить знак кривизны поверхности или рассматривать отрицательные величины y и V.

Из формулы (2) видно, что определитель матрицы преломления  всегда равен единице.

Матрица преобразования лучей для оптической системы.

          Рассмотрим распространение параксиального луча через оптическую систему, состоящую из N преломляющих поверхностей, разделенных N-1 промежутками (рис.5). В качестве первой,  входной, опорной плоскости удобно выбрать плоскость ОП, расположенную на некотором расстоянии слева от первой преломляющей поверхности, следующие опорные плоскости ОП и ОП помещают непосредственно слева и справа от первой преломляющей поверхности, ОП и ОП – с обеих сторон от  второй поверхности и т.д., до тех пор, пока мы не дойдем до плоскостей и , расположенных по левую и правую стороны от  n-ой поверхности. Конечную –  выходную – опорную плоскость ОП помещаем на некотором расстоянии справа от  последней преломляющей поверхности. Переходу от какой-либо  опорной плоскости  к следующей сопоставляем матрицу  . Таким образом, мы получим ряд матриц . Если обозначить вектор луча, прошедшего через опорную плоскость s, как  , то для преобразования параметров луча от  к  можно написать: ,а для всей оптической системы получим 

ряд уравнений

 

 

 

    

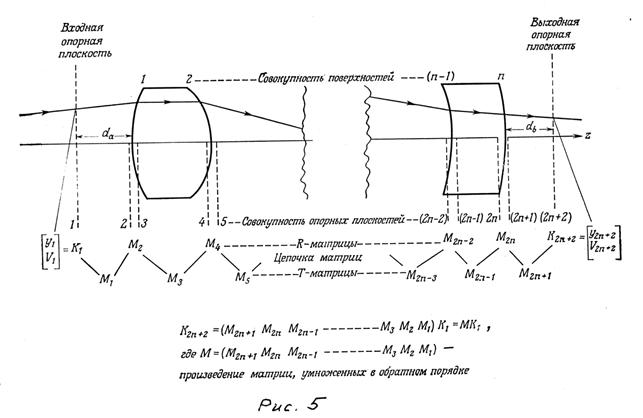
Подставив значение   из первого равенства во второе и используя ассоциативное свойство умножения матриц A(BC)=(AB)C   получим .   Продолжая аналогичные операции получим окончательно

                                     ,

 где матрица

                                 

описывает преобразование лучей, проходящих через оптическую систему. Как видно, эта матрица представляет собой произведение всех матриц, взятых в нисходящем порядке номеров. Полезно зрительно представить себе такой порядок как порядок, который видит наблюдатель, если он смотрит назад от выходной опорной плоскости по направлению к источнику света.

Расчет параметров луча проводится по формуле(1) или (2).

Формулы, полученные выше, можно распространить и на случай отражения. Для этого нужно для отраженного луча считать показатель преломления отрицательным. Так как отраженный луч распространяется в противоположную сторону по отношению к падающему лучу, то для него оптический промежуток также поменяет знак, а значит, матрица перемещения сохранит свой вид.

Так как все матрицы, описывающие поверхности оптической системы, унимодулярные, то и определитель их произведения – матрицы системы—всегда равен единице. Следовательно, если

то имеет место равенство

AD-BC=1                                                                               (4)

и значит только три элемента матрицы независимы.

Так как вид матрицы не зависит от параметров луча, то преобразование любого луча описывается одной и той же матрицей, которая и описывает данную оптическую систему..

Расчет параметров входного луча по данному выходному.

Имеем  умножим слева на  (Обратная матрица, определяемая как , Е – единичная матрица). Получим

Если , то 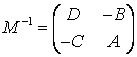 (Верно для матриц 2*2 с определителем, равным единице).

Таким образом:

1) Всю оптическую систему, какой бы сложной она ни была, мы заменяем матрицей, содержащей всего три независимых параметра.

2) Для сложной оптической системы придется вычислять произведение многих матриц. Свойство ассоциативности матриц позволяет по-разному  организовать такое вычисление. Если, например,  часть оптической системы может быть отделена от другой промежутком переменной длины (например объектив и окуляр зрительной трубы), то лучше всего рассчитать отдельно обе части, а затем получить общую матрицу всей системы, как для  двух линз.

Часто бывает удобно не получать общие формулы, а перемножать матрицы численно. При этом полезно время от времени проверять, равен ли единице определитель результирующей матрицы, полученной к данному моменту. Если он окажется не равным единице, это означает, что где-то в процессе вычислений была допущена ошибка.

 Матричная оптика значительно упрощает вычисления, особенно с применением ЭВМ.

Рассмотрим примеры вычисления матриц.

Линза.

Пусть линза сделана из материала с показателем преломления n находится в воздухе, показатель преломления которого считаем равным единице. Пусть первая (по ходу луча) поверхность линзы имеет радиус кривизны , а вторая – ; толщина линзы d.

Оптические силы первой и второй поверхностей вычисляются поформуле  (3) и равны соответственно

  и  .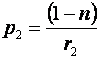

Опорные плоскости расположим  непосредственно перед первой  и за второй поверхностями линзы. Луч света сначала преломляется на первой поверхности, затем проходит между поверхностями и преломляется на второй поверхности. Матрица линзы          вычислится как произведение двух матриц  преломления типа (2) и одной матрицы перемещения типа (1), взятых в порядке, обратном следованию луча:

.

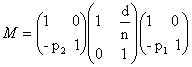Перемножив матрицы, получим

 

 Тонкая линза.

Линза называется  тонкой, если можно считать d=0. Тогда  матрица линзы примет вид

Оптические силы обеих поверхностей просто складываются, и линза действует как одна преломляющая поверхность с оптической силой

.

 

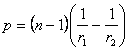Свойства оптической системы.

Мы будем рассматривать оптическую систему как некоторый объект, не вникая в то, из каких элементов она состоит (линзы, промежутки между ними и пр.). Мы знаем только положения вершин крайних поверхностей оптической системы,  значение показателей преломления среды до и после  системы и матрицу системы.

Пусть преобразование лучей оптической системой имеет вид

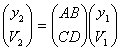  или    

Численные значения элементов матрицы зависят не только от конструкции самой системы, но и от того, где расположены опорные плоскости .

Будем сначала располагать опорные плоскости так, чтобы один из элементов матрицы оказался равным нулю и посмотрим, какой вид будут иметь в этом случае формулы преобразования лучей. Это позволит нам установить ряд важных свойств оптической системы.

1. Сопряженные точки. Изображение. Линейное увеличение.

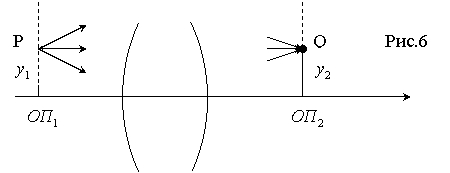
Пусть положение опорных плоскостей выбрано так, что в матрице преобразования лучей  B=0. Тогда  Все лучи, проходящие через какую либо точку Р с координатой  на плоскости   пройдут через одну и ту же точку Q с координатой  на плоскости  (Рис.6), независимо от угла наклона луча. Отсюда следует:

 

          ● Гомоцентрический пучок преобразуется в гомоцентрический.  Точка Q  является изображением точки Р.

          ●  Если предмет лежит в плоскости, перпендикуляоной оси системы, его изображение тоже лежит в плоскости, перпендикулярной оси (опорные плоскости). Плоскости  и  будут взаимно сопряженными плоскостями.

● Отношение  называется линейным увеличением системы. Если  – изображение прямое, если  – обратное

Так как AD=1, то D=1/A

● Изображение подобно предмету ( – увеличение не зависит от )

● Чтобы найти положение изображения какой-либо точки, нужно поместить первую опорную плоскость на месте объекта, вторую – на некотором расстоянии от оптической системы, найти матрицу такой конфигурации и в полученной матрице положить B = 0.

Изображение в тонкой линзе

Пусть, например, предмет находится на расстоянии a от тонкой линзы с оптической силой p. Нужно найти положение изображения. Поместим вторую опорную плоскость на расстоянии b от линзы справа от нее. Матрица преобразования лучей будет

                       

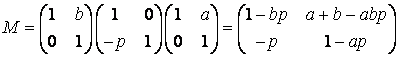
Положив В=0=a+b-abp получим  соотношение между положением предмета и изображения : . Увеличение

2. Фокусы оптической системы. Фокальные плоскости.

Если положение опорных плоскостей выбрано так, что

 D=0,

.

Все лучи, выходящие из одной точки  выйдут из оптической системы под одним и тем же углом  независимо от того, под каким углом  эти лучи  входили в систему (Рис. 7). Плоскость называется в этом случае первой (передней) фокальной плоскостью системы, а точка – первым (передним) фокусом. Точка пересечения передней фокальной  плоскости осью системы называется  передним главным  фокусом. Все лучи, проходящие через передний главный фокус системы (=0), выходят из нее параллельно оптической оси (= 0).

Если

A=0,

.

Все лучи, входящие в систему под одним и тем же  углом , пройдут через одну и ту же точку  на выходной опорной плоскости . Таким образом, система собирает пучек параллельных лучей в фокус в точках, расположенных на плоскости , которая называется второй (задней) фокальной плоскостью оптической системы. Точка пересечения задней фокальной плоскости осью системы называется  главным задним фокусом. В этой точке собираются лучи, входящие в систему параллельно оптической оси.

          Для тонкой линзы:

(Положения фокусов – на одинаковом расстоянии от поверхностей линзы. Если р>0, то передний фокус – слева, т.к. расстояние фокальная точка – поверхность линзы – положительно)

3. Телескопическая система. Угловое увеличение.

Пусть

 C=0,

        и, если по обе стороны системы воздух,  n=1, то

 Все лучи, которые входят в систему параллельно друг другу (например, под углом  оптической оси) на выходе оптической системы образуют также параллельный пучек лучей, но относительно оси его угол наклона изменится и станет равным v_2 (рис.8).Такая система линз, которая преобразует параллельный пучек лучей в параллельный же, называется  афокальной или  телескопической системой. В этом  случае отношение углов называется угловым увеличением оптической системы:

                                                       

 

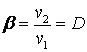
4.     Главные точки. Главные плоскости. Фокусные расстояния.

Пустим на ОС луч, параллельный оптической оси. Пройдя ОС этот луч (или его  продолжение) пересечет  ось в точке  – заднем главном фокусе системы (Рис 11). Продолжим оба луча – входящий в систему и выходящий из нее – и найдем точку их пересечения. Плоскость , проведенная через    эту точку  перпендикулярно оси, называется  второй (задней) главной плоскостью  оптической   системы, а точка  пересечения ее с осью называется  второй (задней) главной точкой. Найдем отрезок . Из формул преобразования лучей

 Имеем (Так как )

Из чертежа: , откуда , или, если ОС находитс в воздухе,

                                                        

Отрезок  (его длина и направление) не зависит от , он характеризует систему. Он называется заднее фокусное расстояние системы.

Так как C=-p, то заднее фокусное расстояние равно обратной величине от оптической силы системы .

Оптическая сила измеряется в диоптриях. Одна диоптрия равна 1/м, так что линза с оптической силой, например, в 2 диоптрии имеет фокусное расстояние 50 см.

Аналогично:  Рассмотрим луч, выходящий из ОС параллельно оптической оси. Этот луч до системы пройдет через передний фокус. Найдем точку пересечения луча «до» и «после» – передгяя (первая) главная точка – опустим перпендикуляр на ось ( через него прохолит перелняя главная плоскость) и найдем отрезок  (на чертеже он отрицательный, так как направление его –  против направления света) переднее фокусное расстояние оптической системы.. Из чертежа . Или 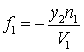.  Обратное преобразование луча имеет вид , откуда   

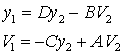
или  . Таким образом, , или, если ОС находится в воздухе

                                                          

 

          Главные плоскости оптической системы — сопряженные плоскости с единичным коэффициентом усиления .

Главные точки (и фокусы) могут по-разному располагаться относительно самой системы. Например, у системы двух собирающих линз может быть так:

 

 

 

 

         

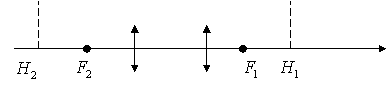
Hазвания «передний» и «задний» в обозначении главных и фокальных точек до некоторой степени условны. Если систему повернуть на 180◦ вокруг вертикальной оси, а направление распространения света оставить прежним, то передняя и задняя поверхности поменяются местами. Реальная оптическая система обычно рассчитана на определенное направление лучей, этим и определяется, какая из кардинальных точек будет передней, какая – задней.

Вместо реальной оптической системы для построения лучей достаточно рассмотреть так называемые кардинальные точки — точки пересечения оптической оси с двумя фокальными плоскостями и двумя главными плоскостями.

          Оптическая система ведет себя так, как будто пространство между главными плоскостями отсутствует, а в месте стыка установлена тонкая линза.

 

Главные и фокальные точки называются кардинальными точками оптической системы. Такое название они получили потому, что, зная расположение кардинальных точек и положение объекта относительно них, можно найти положение и величину изображения, и при этом совершенно не нужнознать, из каких элементов состоит оптическая система, как идут лучи внутри нее и даже – как она расположена относительно своих кардинальных точек.

5. Построение изображения.

Положение изображения можно найти геометрическим построением. Пусть для оптической системы задано положение главных плоскостей  и    и главных фокусов  и  (рис. 12). Найдем изображение отрезка  перпендикулярного оптической оси. Для этого проведем луч из точки  параллельно оптической оси до его пересечения со второй главной плоскостью в точке . По выходе из системы этот луч должен пройти через точку  т.е. он пойдет понаправлению . Второй луч проведем через точки  и продолжим его до пересечения с первой главной плоскостью в точке .

 

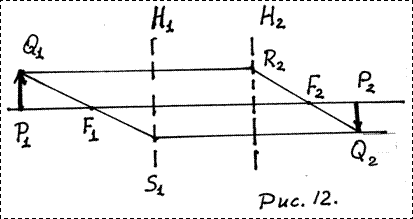
По выходе из системы этот луч будет параллелен оси. Продолжим оба луча до их пересечения в точке . Эта точка и будет изображением точки , а отрезок , перпендикулярный оси, будет изображением отрезка .

В практических задачах мы чаще всего определяем положение объекта и изображения не по отношению к главным плоскостям, с которыми не связана

никакая материальная среда отсчета, а расстоянием  от первой (для объекта) и от последней (для изображения) поверхностей системы. Поэтому и кардинальные точки необходимо “привязать” к крайним поверхностям оптической  системы. Таким образом, чтобы полностью охарактеризовать идеальную оптическую систему, находящуюся в воздухе, достаточно четырех величин. Можно, например, указать оптическую силу, передний и задний фокальные отрезки (расстояние от крайней поверхности системы до фокуса) и толщину системы, т.е. расстояние от передней до задней поверхности.

          Главные плоскости оптической системы — это сопряженные плоскости с единичным коэффициентом увеличения . Это видно из построения. Действительно, построим изображение точки . Для этого воспользуемся лучом , параллельным оптической оси, и лучем , проходящим через фокус. После прохождения системы лучи пересекутся в точке .

Мы показали, что оптическую систему, сколь угодно сложную, можно в некотором смысле заменить тонкой линзой (построение изображения  в идеальной ситстеме происходит по тем же правилам). Поэтому нет смысла рассматривать сложные системы, в некоторых (частых!) случаях их можно без потери смысла заменить тонкой линзой. Что мы в дальнейшем и будем делать.