Временная и
пространственная когерентность
Ранее
мы получили условие, определяющее характер интерференции в виде
(1)
(2)
О
степени когерентности двух лучей можно судить по видности V интерференционной
картинки. Если интенсивности интерферирующих лучей одинаковы, то 
. Однако на практике всегда V<1, т.е. два луча не вполне когерентны. Основные
причины этого две: разность фаз двух колебаний никогда не бывает совершенно
постоянной и источник света никогда не бывает точечным, он всегда имеет
конкретные размеры.
Соответственно вводят пространственную
и временную
когерентность.
Временная
когерентность.
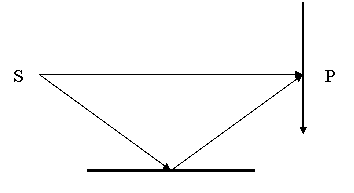
Пусть свет идет от одного и того же точечного
источника, но лучи света проходят разные расстояния (возможно, проходят в
разных средах с разными показателями преломления). Например, по такой схеме (это – зеркало Ллоида). Будем считать
свет квазимонохроматическим с постоянной амплитудой, но меняющейся фазой. Тогда
в угловых скобках выражения (1) (усреднение по времени) стоит одна и та же начальная фаза, но
определенная в разные моменты времени.
Эти фазы вообще говоря, разные (они
непрерывно меняются во времени), так что при усреднении получается V<1 и
только если Δt=0 , то V=1. Однако, чем меньше будет Δt, тем
большая связь между фазами и тем больше степень когерентности
Введем время когерентности 
Если Δt<< – колебания когерентны
Если Δt>> – колебания не когерентны
Если Δt ≈ – колебания частично
когерентны
Каков смысл времени
когерентности? Вспомним модель излучающего тела (газа).Это излучение можно
представить как ряд гармонических колебаний, длящихся некоторое время τ, а
затем возникает новое колебание с той же частотой, той же (примерно)
амплитудой, но другой (непредсказуемой!) начальной фазой. Время τ – это
время жизни возбужденного атома. Но это же время и является временем
когерентности. Такая волна состоит из последовательности цугов – отрезков синусоидальных волн длиной l=cτ . (для простоты считаем коэффицент преломления равным
единице) Длина l это длина когерентности.. Если разность
хода лучей 
, то колебания когерентны, если 
– не когерентны. Это –
условие, накладываемое на разность хода в интерференционных опытах. Условие
исчезновения интерференционной картины 
.Поэтому все интерференционные приборы выполнены так, чтобы
разность хода была небольшой.. В реальных (тепловых) источниках света 
и значит длина когерентности около
Геометрическая интерпретация.
Когерентность во времени это когерентность по линии
луча. Рассмотрим какой-либо луч, испускаемый точечным источником S (Рис.13). Источник испускает цуги волн, их границы в
некоторый момент времени показаны на рисунке пунктиром. Эти границы
перемещаются по лучу со скоростью света. Если рассмотреть 2 точки пространства,
находящиеся на луче на расстоянии, большем длины цуга (S1 и S2), и
каким-либо образом свести поля в этих точках, то интерференции не будет, так
как эти поля не когерентны. Если же взять две точки более близкие (S1 и S3), то такие
поля будут принадлежать некоторое время к одному цугу, и только когда граница
между цугами проходит между этими точками – к разным цугам. Поэтому поля будут
частично когерентными, и степень когерентности будет тем больше, чем ближе
расположены эти точки.
Время когерентности можно измерить экспериментально, если
изменять разность хода лучей и наблюдать, как меняется видность
интерференционной картины Однако нам удобнее ввести вместо времени
когерентности какую-либо другую величину, которую удобно измерять. Оказывается,
временная когерентность тесно связана с монохроматичностью света.
Когда мы рассматривали разложение излучения в спектр, мы
видели, что в результате того, что излучение атома не бесконечно, а длится
некоторое время τ, спектральная линия не строго монохроматична, а имеет
контур (зависимость интенсивности от частоты) колокообразной формы, форма этого
колокола – контур линии – зависит от процессов, которые определяют время жизни
возбужденного атома , но полуширина
этого контура во всех случаях определяется соотношением 
или 
.Величина τ здесь играет роль времени когерентности. Таким образом, время когерентности связано с
монохроматичностью колебаний, способных образовать интерференционную картину: 
. А длина когерентности равна 
. Условие существования интерференционной картины 
.. Но разность хода лучей определяет номер полосы
интерференции 
. А 
. Таким образом, максимальное число полос, которое можно
увидеть определяется из соотношения 
, что дает 
. Чем выше порядок интерференции, тем уже должен быть
спектральный состав источника света. И наоборот – предельный порядок, который
можно наблюдать от данного источника
Например в тонких пленках 
и, значит 
, так что источником может быть белый свет. Дальше мы
познакомимся с приборами, для которых порядок интерференции велик. Такие
приборы требуют света высокой монохроматичности источника света.
Замечание. Наглядный
смысл последнего равенства таков. Пусть имеется источник, излучающий свет в
пределах от λ до λ+Δλ. Тогда для каждой длины волны
запишется так 
. Для разных волн максимумы порядка m и интерференционная картина окажется
смазанной, размытой. Это размытие будет тем больше, чем больше интервал длин
волн Δλ. В том случае, когда
максимум порядка m для длины
волны λ+Δλ наложится на максимум порядка m+1 для длины волны
λ, картина полностью смажется так, что максимумы будут не видны.
Таким образом, условие исчезновения интерференционной картины m(λ+Δλ)=(m+1)λ. Раскрывая скобки, получим
mλ+mΔλ=mλ+λ, откуда 
.
Пространственная
когерентность.
Это
– когерентность света в направлении перпендикулярном к лучу, поперек луча. Это
когерентность полей в разных точках волновой поверхности.
Геометрическая интерпретация показана на рис.14. Рассматривается когерентность
полей в точках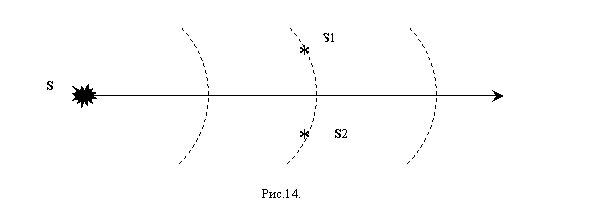
S1 и S2. Так как они
лежат на одном волновом фронте (показан пунктиром), то 
. Казалось бы,
когерентность должна быть полной, так как фазы рассматриваются в один и тот же
момент времени t, но это не совсем так. Дело в том, что реальный
источник света не строго точечный, поэтому поверхность разных фаз «дрожит»,
испытывает шумовые повороты, вызываемые тем, что свет в точку наблюдения
приходит то от одной, то от другой точки источника. (Если бы источник света был
точечным, то, конечно, поля в точках S1 и S2 были полностью когерентны).
Рассмотрим для наглядности
схему опыта Юнга (рис.15). Возьмем в качестве источника света S полоску шириной 2b постоянной яркости. Дальше поставим экран с двумя отверстиями
S1 и S2. Считаем свет
достаточно монохроматическим, чтобы получить четкую интерференционную картину
от точечного источника, и наблюдение ведем около оси, так что разность хода
интерферирующих лучей близка к нулю. Если бы поля в точках S1 и S2 были
полностью когерентны, мы получили бы на экране вполне четкую интерференционную
картину (видность полос равнялась бы единице). В действительности картина
получается размазанной. Видность интерференционной картины соответствует
когерентности полей в точках S1 и S2. Посмотрим,
как видность интерференционной картины зависит от размера источника света b. Отдельные
бесконечно малые участки источника S дают
четкую интерференционную картину. Но каждая точка источника дает свою
интерференционную картину, все они одинаковы, но немного сдвинуты друг
относительно друга. Так как отдельные точки источника являются некогерентными источниками, то эти
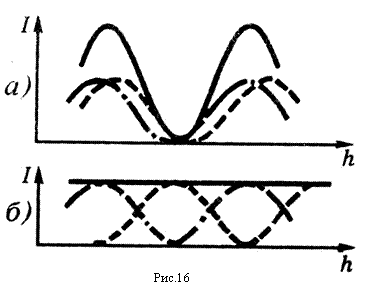
отдельные картинки просто складываются по интенсивности. В результате интенсивность
в минимуме не равна нулю (Рис.16а). С увеличением размера источника картинка
становится всё менее четкой, и полосы пропадают (видность V=0) если минимумы одной половины источника налягут на
максимумы другой половины, т.е. расстояние
изображений крайних точек источника равно ширине полосы (рис.16б). При
дальнейшем увеличении источника полосы опять появятся, но будут менее
контрастны.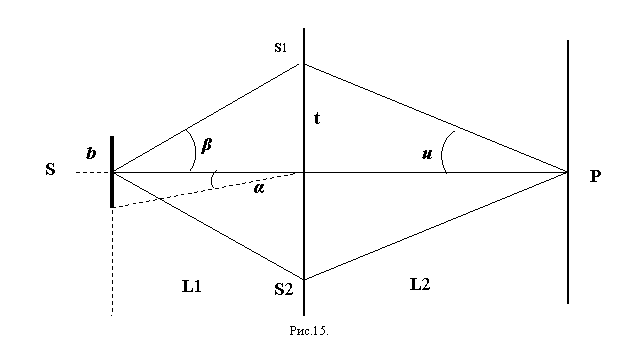 
Как видно из рис. 15
при переходе от одной точки источника к другой разность хода может
измениться только слева от экрана со щелями. Выясним, какому перемещению b по ширине полоски источника соответствует изменение
разности хода на λ. Представим себе, что свет идет справа налево. Тогда
слева получим интерференционные полосы и
переход от одной полосы к другой и соответствует
изменению разности хода лучей на λ
– это как раз то, что нам нужно. Для ширины полосы мы получали раньше
– это для полосы
справа. Если принять за точечный источник перемещен в точку P, то то слева появились бы полосы шириной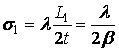 
, таким образом, условие полного исчезновения полос будет 
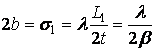. Обычно за допустимые размеры источника света принимают
размер вдвое меньший
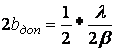, при этом видность равна примерно 2/3. При дальнейшем
увеличении размера источника (2b>λ/2β) опять
появятся не резкие (так как будут видны на равномерном светлом поле от
центральной части источника) полосы, они опять пропадут при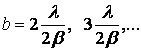 
Зависимость
видности полос от размера источника света показана на рис.17.
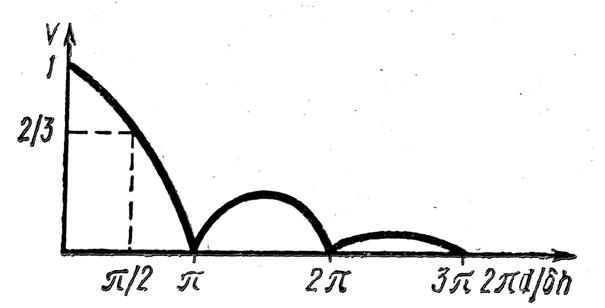
Рис.17
Определим угловые размеры источника света. Из
чертежа рис.15 видно, что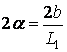 
. Но картинка полностью смазывается при 
, следовательно условие исчезновения интерференционной
картинки будет
.
Это можно трактовать так. Величина 2t определяет размер области когерентности света в месте
расположения экрана с отверстиями. Если расстояние 2t больше области когерентности, то свет от таких точек
не дает интерференционной картины, так как поля в точках S1 и S2 некогерентны.
Последняя формула позволяет
определять угловые размеры звезд по размеру области пространственной
когерентности света звезды на поверхности Земли (угловой диаметр звезд
настолько мал, что его нельзя измерить непосредственно наблюдая изображение
звезды в телескоп).. Для измерения углового диаметра звезды Майкельсон создал прибор, который так и
называется – звездный интерферометр Майкельсона.
Звездный интерферометр Майкельсона.
Угловой
диаметр звезды очень мал, так что ни один из существующих телескопов не дает
возможности наблюдать изображение звезды – вместо этого мы видим дифракционное
пятно, диаметр которого зависит от диаметра объектива телескопа и никак не
связан с размером звезды. Представим себе, что точка S на рис.15 – это звезда, а точки S1 и S2 – две точки
на Земле, освещаемые этой звездой. Мы можем свести волны от этих двух точек и
посмотреть, будет ли интерференционная картина. Это и делает звездный
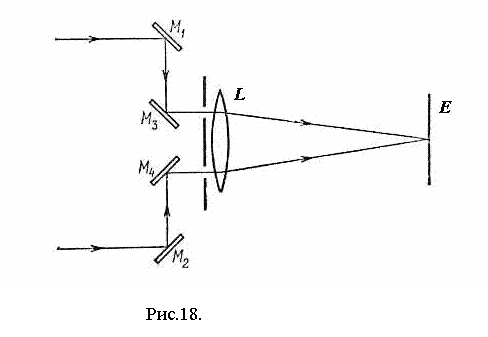
интерферометр придуманный Майкельсоном. Он устроен так (рис.18). Свет звезды падает на внешние (не в телескопе) зеркала М1
и М2, отражаются далее от двух зеркал М3 и М4, и, проходя через два отверстия в
диафрагме, попадают на объектив и формируют изображение на плоскости Е, где и
наблюдается интерференционная картина от двух изображений. Пусть α –
угловой диаметр звезды, d – расстояние
между зеркалами М1 и М2 (они соответствуют точкам S1 и S2 на рис.15).
Условие наличия интерференции будет d<λ/α (точнее –
d<1,22λ/α, так как звезда – не квадрат, а диск). Наблюдаем
картину при разных расстояниях d. Найдя такое
расстояние, при котором интерференционная картина исчезает, можем вычислить
α. Майкельсон измерил таким
образом угловой диаметр звезды Беттельгейзе (α-Ориона) и получил
α=0,047” Для этого ему понадобилось расстояние (база) около трех метров:
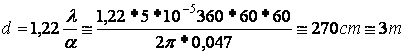
Для большинства звезд база должна быть больше.
Но настройка интерферометра с большой базой – очень сложная технически задача.
Кроме того, на изображение влияет неоднородность атмосферы (турбулентность).
Это все ограничивает возможности измерений.
По этому же принципу устроены радиоинтерферометры.
Здесь длина волны значительно больше –
порядка
