3

Отражение света от металлической поверхности. Оптические характеристики металлов.

Металлическая поверхность имеет большой коэффициент отражения. Это обусловлено наличием в металлах большого числа «свободных» электронов (т.е. электронов не связанных с конкретным атомом, а могущих перемещаться внутри кристаллической решетки металла). Вторичные волны, обусловленные вынужденными колебаниями этих электронов, ведут к образованию сильной отраженной волны (отражается 95% и больше) и слабой волны, идущей внутрь металла. Та часть световой энергии, которая проникает внутрь металла, испытывает в нем поглощение (за счет потерь на Джоулево тепло – взаимодействие свободных электронов с ионами решетки). Какая доля света отражается, а какая проходит внутрь и поглощается – это зависит от проводимости металла. В «идеальном» проводнике поглощение равно нулю, но падающий свет полностью отражается и внутрь ничего не проходит. К этому приближается чистая поверхность серебра, натрия. Железо отражает 30-40% падающего света.

При сравнительно небольших частотах (ИК) оптические свойства металла обуславливаются главным образом поведением свободных электронов. При переходе к видимому и УФ свету начинают играть роль также связанные электроны, характеризующиеся собственной частотой, лежащей в области более коротких длин волн. Коэффициент отражения в этой области сильно зависит от частоты.

Полная теория прохождения света через металлы и отражения от их поверхности должна учитывать все эти особенности. Это тем более трудно, что электронная теория металлов требует применения квантовой механики. При упрощенной трактовке вопроса, основанной на электромагнитной теории Максвелла, задача сводится к учету проводимости металла, то есть к введению формально в уравнения Максвелла члена, зависящего от коэффициента электропроводности σ. Уравнения Максвелла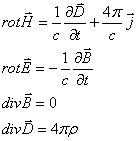

Считаем по-прежнему, что среда изотропна и однородна, электрически нейтральна. Значит

, , ρ=0, μ=1(для оптических частот это выполняется даже для магнетиков). Но σ≠0 !!. Нас интересует первое из уравнений (9.1). Подставим сюда соотношение j=σE. Получим

Оно отличается от случая диэлектрика наличием члена, содержащего σ. Мы будем рассматривать плоскую монохроматическую волну , тогда и .. Подставив это в (1) получим

Полученное выражение отличается от случая диэлектрика только тем, что вместо вещественной величины диэлектрической проницаемости стоит комплексная величина

, (2)

следовательно, мы можем использовать все соотношения, полученные ранее для диэлектриков, заменив ε на . Насколько существенна мнимая часть по сравнению с действительной? Сделаем численную оценку для меди. Медь – хороший проводник. Её удельное сопротивление равно .

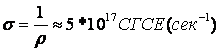
Тогда , а – оптическом диапазоне. Таким образом, получаем, что . Но ε порядка единицы, и, получается, что мнимая часть много больше действительной. На практике электропроводность для высоких (оптических) частот значительно меньше, чем в статическом случае. Для типичных металлов и в формуле (2) существенна как действительная, так и мнимая часть.

Если диэлектрическая проницаемость комплексная, то комплексным будет и показатель преломления. Запишем его так:

– величина порядка единицы (видно из-за оценки слагаемых в формуле (2))

Чтобы выяснить физический смысл вернемся к выражению для плоской волны

Волновое число – комплексное:

Мы уже имели дело с комплексным волновым числом и видели, что мнимая часть означает наличие затухания амплитуды волны.

Это – затухающая волна. Величина κ – коэффициент затухания. Здесь в отличие от полного внутреннего отражения затухание связано с поглощением, т.е. переходом энергии излучения в другие виды энергии.

Так как интенсивность пропорциональна квадрату амплитуды, то для интенсивности получим

или Это – закон Бугера. (Он применяется вообще к любым поглощающим средам). Коэффициент поглощения α обычно (при не слишком больших интенсивностях) не зависит от интенсивности I , но он всегда зависит от длины волны. Коэффициент поглощения может быть и отрицательным, α<0, это соответствует усилению света ( например, в лазерах).

Глубина проникновения э-м волны в металл.. За неё принимается такая глубина. d, на которой амплитуда уменьшается в e раз.

Для металлов κ– величина порядка единицы, обычно больше единицы. Это значит, что волна проникает на глубину, меньшую длины волны, т.е. никакого периодического изменения поля внутри металла нет.

Два параметра, n и κ, являются константами, характеризующими оптические свойства металла. Два параметра – ε и σ – характеризуют его электрические свойства. Мы можем связать оптические характеристики с электрическими. Имеем

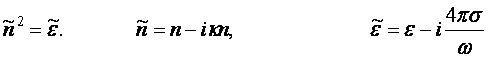откуда получаем, возводя n в квадрат

Приравняв отдельно действительную и мнимую части, получим

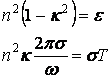
Решив эти уравнения, можно перейти от оптических характеристик к электрическим, или наоборот.

«Совершенный» с точки зрения электродинамики проводник характеризуется бесконечной проводимостью. Какие при этом n и κ? Разделив одно из предыдущих равенств на другое, получим

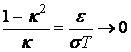
Следовательно, и, так как , то . Всё поглощается на бесконечно малом пути. Реально показатель преломления далек от бесконечности, часто он даже меньше единицы. Заметим, что для высоких частот (видимый и ультрафиолетовый свет) все четыре величины, характеризующие металл, n,ֵ κ, ε, σ зависят от частоты и только для низких частот электропроводность σ приближается к значению, полученному для постоянных полей.

Коэффициент отражения электромагнитной волны от металла получим, подставив в формулу для коэффициента отражения выражение Так как показатель преломления комплексный, берем отношение квадратов модулей. Получим

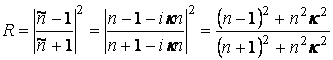
Если сравнить с диэлектриком,

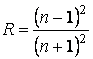, то видно, что коэффициент отражения от металла больше, чем от диэлектрика с таким же показателем преломления n. Кроме того – чем больше мнимая часть в выражении для , тем больше и коэффициент отражения! Металлы хорошо отражают видимый свет. Значит мнимая часть их показателя преломления очень велика. Однако мы видим, что большая мнимая часть показателя преломления означает сильное поглощение. Таким образом, имеется общее правило – если какой либо материал оказывается хорошим поглотителем при какой то частоте, то отражение волн от его поверхности на этой частоте велико и очень мало световой энергии попадает внутрь. Отражение от поверхности металла имеет характерный «металлический» блеск. Подобный же эффект можно наблюдать на сильных красителях. Чистые кристаллы самых сильных красителей имеют металлический блеск. Это можно наблюдать, например, у засохших чернил. Фиолетовые чернила имеют золотистый оттенок, красные – зеленый. Объяснить это можно так. Красные чернила поглощают из проходящего света зеленые лучи, так что если концентрация чернил очень велика, они будут давать сильное поверхностное отражение при частое зеленого света. Наоборот, если концентрация красителя не так велика (разведенные чернила, цветное стекло), то в отражении мы видим тот же цвет, что и на просвет. Это потому, что мы видим свет, прошедший внутрь материала и отразившийся от неоднородностей внутри него и от противоположной поверхности. Здесь зеленые лучи (в красных чернилах) поглотились, а красные вышли и блеска такого нет.