Интерференция света.

Интерференция волн – явление усиления или ослабления амплитуды результирующей волны в зависимости от соотношения между фазами складывающихся в пространстве двух (или нескольких) волн. Интерференция  имеет место для всяких волн, в том числе и для световых.

         В оптике наблюдают обычно не амплитуду, а интенсивность света. Вспомним основные определения.

1.     Интенсивность определяют обычно с точностью до постоянного множителя. Она равна ,    где E(t) – электрическое поле волны,  – момент наблюдения,  – время усреднения.

2.     Стационарность. Мы будем рассматривать только стационарные процессы т.е. интенсивность не зависит от времени. Это значит, что интенсивность не зависит от выбора нижнего предела интегрирования.

3.     Неопределенность. Интенсивность зависит от времени усреднения. В оптике обычно это время определяется инерционностью прибора, т.е. равно около 0,1 сек.

Усреднение будем записывать так . В комплексной записи .Для монохроматической волны   – интенсивность пропорциональна квадрату амплитуды

Рассмотрим самый общий случай. Пусть в некоторой точке пространства одновременно существуют две произвольных электромагнитных волны и электрические  поля их равны  и  (Это – реальные поля, не в комплексной записи). Согласно принципу суперпозиции результирующее поле равно сумме этих полей , и интенсивность

                                        

или

Член  – интерференционный. Если он равен нулю, то интенсивности просто складываются, интерференции нет. Говорят, что поля не когерентны. Например, некогерентно излучение отдельных атомов (молекул) в излучающем теле Этот случай мы рассматривали в разделе “модель излучающего тела”. Если интерференционный член не равен нулю, то результирующая интенсивность не равна сумме интенсивности от каждого поля. Имеет место интерференция. Говорят, что поля когерентны (частично, или полностью).

Заметим

1. Само понятие когерентности относительно, т.к. интенсивность зависит от времени усреднения .

2. Из формулы (1) следует, что если волны поляризованы во взаимно перпендикулярных плоскостях, то интерференции нет. Но может быть “скрытая” интерференция.

Рассмотрим наиболее важные частные случаи.

 

1.     Интерференция монохроматических волн.

`        Будем рассматривать  два точечных источника монохроматических волн одинаковой частоты.( и на рисунке 1). Пусть волны одинаково поляризованы, например так, что электрический вектор перпендикулярен плоскости рисунка. Колебания в точках  и  имеют вид

 

.

Здесь  и – начальные фазы.

В точке P эти волны приобретут дополнительную фазу и будут иметь вид

Здесь мы пренебрегаем геометрическим фактором – уменьшением амплитуды с расстоянием.

Рассмотрим результат интерференции этих волн. Согласно формуле (1)

. Раскрываем косинус разности и перемножаем

При усреднении по времени учтем, что фазы  и  – постоянны, последний член в сумме равен нулю, а среднее значение квадрата косинуса (синуса) равно 1/2. Получим

Но  Точно так же и для второго поля. Поэтому

   и . Окончательно получим

или, подставляя значения фаз,

Обозначим

. Величина  – это оптическая разность хода лучей.

Если, как это часто бывает, оба луча распространяются в воздухе, то просто .

Таким  образом  

                                                                                     (2)

                                                                                           (3)

         В выражении (3) два слагаемых. Первое – разность фаз, приобретенная лучами на пути от источников до точки наблюдения – зависит от прибора. Второе – разность начальных фаз – зависит от процессов в источниках света.  Для монохроматических источников вторая часть постоянна. Положим ее равной нулю. Тогда – интенсивность света в точке наблюдения зависит от разности хода лучей.

Интенсивность будет максимальной при  .

      Интенсивность света от двух источников больше, чем сумма их интенсивностей.      Но  или  

Амплитуда суммарной волны равна сумме амплитуд складываемых волн

Интенсивность будет минимальной при 

       или . Если амплитуды равны, то I=0.

Итак: интенсивность меняется  в пространстве в зависимости от разности хода лучей.  Электрическое поле меняется от  (когда cos=+1) до (когда cos=-1).  Таким образом, складываются не интенсивности, а амплитуды колебаний.

Вычислим распределение интенсивности вдоль линии, параллельной  прямой, соединяющей источники света (рис.2). Будем считать L>>2t  L>>x,  где 2t – расстояние между источниками света, а х – расстояние точки наблюдения от центра интерференционной картины. Для простоты  положим  и . Тогда

 

Второе расстояние подсчитывается аналогично

,

Подставив это в выражение для интенсивности, получим

Распределение интенсивности имеет вид синусоиды. На экране будет видно чередование темных и светлых полос. Максимальная интенсивность , минимальная .

         Ширина полосы интерференции .. Введем угол схождения лучей 2u – угол, под которым сходятся в точке наблюдения два луча от первого и второго источников света. Тогда

Замечания.

1.     Закон сохранения энергии выполняется, т.к. имеет место просто перераспределение интенсивности в пространстве.

2.     Постоянная добавка разности начальных фаз в выражении для означает сдвиг всей интерференционной картины вдоль оси x на постоянную величину. Ширина полосы при этом сохраняется.

3.     Если интенсивности двух источников неодинаковы, , то минимумы не равны нулю, полосы видны на постоянном светлом фоне. Ширина полосы сохраняется.

2.     Интерференция квазимонохроматических волн.

Этот случай имеет большое практическое применение. Если взять два независимых источника света (даже если пропустить этот свет через поляризатор и светофильтр) и наблюдать наложение волн, интерференции не получится. Причина в том, что реальные волны никогда не бывают монохроматическими. Даже излучение одного атома, излучающего одну спектральную линию – не бесконечная синусоида, т.к. возбужденный атом имеет конечное время жизни. В реальном источнике света излучает сразу много атомов и фазы колебаний в их излучении никак не согласованы. В двух источниках излучают два разных набора атомов и разность фаз этих волн хаотически меняется. Меняется, конечно, и амплитуда, но эти изменения не очень сильные. Поэтому будем рассматривать квазимонохроматические волны с постоянными амплитудами (принципиально это мало что изменит, а рассмотрение проще). Итак

где  (со значками «1» и «2»). Второе слагаемое постоянно для данной точки наблюдения, а начальные фазы  медленно по сравнению с периодом колебаний, (но не по сравнению с временем наблюдения!) меняются. В каждый момент времени объективно существует «мгновенная» интерференционная картина, определяемая формулами (2) и (3), где  – значение фазы в момент t:

    зависит от времени  и, значит

                                             

Мы наблюдаем некоторую среднюю (за время наблюдения) интенсивность

                                                             

         

Если разность  остается постоянной, то этот случай ничем не отличается от случая монохроматических волн.                             

Таким образом, необходимое условие наличия четкой интерференционной картины (в случае квазимонохроматических волн с постоянными амплитудами) –  разность фаз двух складываемых колебаний сохраняет свое значение за время усреднения, хотя сама фаза может меняться (хотя бы и хаотически и в больших пределах). Это свойство широко применяется в оптике для осуществления интерференционных схем.

         Пусть, однако, разность фаз не остается постоянной. Тогда интерференционная картина размывается. Действительно, хотя в «мгновенной» интерференционной картине распределение интенсивности синусоидальное, но положение центра светлой (и, соответственно, темной) полос постоянно меняется, картинка «гуляет» по экрану, а мы наблюдаем некоторое среднее ее значение. Поэтому максимумы будут не столь интенсивны, а минимумы интенсивности не равны нулю. Насколько размыта картинка зависит от того, как меняется разность фаз. Если разность  меняется незначительно, то картинка может быть более или менее четкой (частично когерентные источники света), если же фазы совсем не согласованны между собой, то разность может принимать всевозможные значения, меняясь хаотически и принимая то положительные. то отрицательные значения, и тогда интерференционная картина исчезает совсем (некогерентные источники).

Формула для интенсивности получается такой

Чтобы получить формулу (7) запишем усреднение в (6) в комплексной форме.

,

Если возьмем реальную часть от начального и конечного выражений, получим

где

 – это результат усреднения по времени. Величины /γ/ и Φ нам неизвестны (если неизвестен закон изменения фазы со временем), но ясно, что чем больше корреляция между значениями начальных фаз, тем больше /γ/. Таким образом, величина   /γ/ , , характеризует, насколько «смазана» картина. а Ф – фаза, которая получилась в результате усреднения в выражении (6) (полосы могут не только размазаться, но и сместиться).

Экспериментальной количественной оценкой согласованности фаз и, следовательно, когерентности колебаний, может служить видность интерференционной картины. Она равна

                                                  

Для полностью когерентных источников света одинаковой интенсивности V=1, если источники не когерентны, V=0, в промежуточных случаях 0<V<1 Если  , то V=/γ/.

Осуществление когерентных колебаний в оптике.

Интерференционные схемы.

Мы видели, что для получения когерентных волн (и, значит интерференционной картины) два разных источника непригодны. Френель (1818г) показал, что для этого можно использовать излучение одного и того же источника света. Необходимо испускаемое излучение разделить на два потока, распространяющихся по разным путям (возможно – в разных условиях), а затем свести их вместе. Тогда разность начальных фаз останется постоянной т.к. это волны от одного и того же источника. Необходимо только, чтобы разность времен  была небольшой, чтобы фаза колебаний за это время не успела заметно измениться.

         Можно делить поток излучения по-разному. Различают: а) деление фронта волны и б) деление амплитуды волны.

 

 

Деление фронта волны.

Примеры таких  интерференционных схем:      опыт Юнга, бипризма Френеля, бизеркала Френеля, билинза Бийе. Эти и другие подобные схемы описаны в любом учебнике по оптике и здесь они не приводятся.

  Основные  характеристики интерференционных схем.

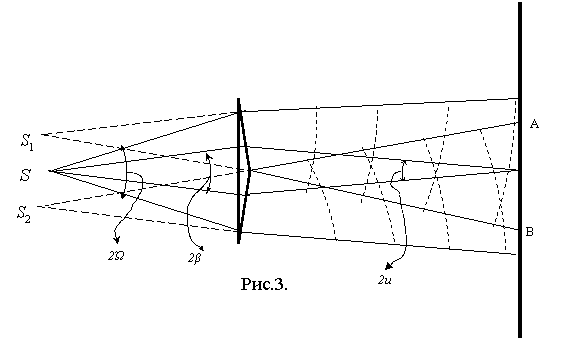
 Мы их рассмотрим на примере бипризмы Френеля (рис.3.).

 

1.  В каждой интерференционной схеме свет от источника S делится на два пучка. Эти пучки определяют два вторичных источника  

2.   Интерференция наблюдается в области АВ, где перекрываются пучки лучей, идущих от источников , это поле интерференции.                                                          3.  Средняя освещенность поля интерференции зависит от телесного    угла Ώ, в    котором распространяются лучи каждого пучка.

4.  Угол 2β, под которым расходятся два интерферирующих луча – апертура интерференции – важен, т.к. определяет допустимые размеры источника света.

5.  В поле интерференции углу 2β соответствует угол схождения лучей 2u. Этот  угол определяет ширину полосы интерференции σ. Ранее мы получили:.

Так как интерференционная картина имеет вид полос, перпендикулярных оси картинки (плоскости чертежа), то точечный источник S  можно заменить узкой щелью. Вид картинки (по крайней мере, вблизи её центра) не изменится, а общая интенсивность  станет больше. Это относится и ко всем показанным схемам.

Деление амплитуды волны.

Интерференция в тонких пленках.

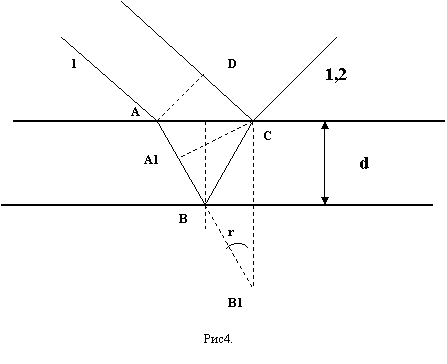
Рассмотрим отражение света от тонкой прозрачной пленки с показателем преломления материала n. Плоская волна падает на пленку под некоторым углом . Возникают два луча, отраженные от первой и второй поверхностей (рис.4).  Разность хода лучей 1 и 2  равна Δ=n(ABC)-DC+λ/2. (прибавление половины длины волны возникает за счет отражения света от более плотной среды). Так как волновой фронт

в первой среде (воздухе) – AD, а в материале пленки – A1C, то время прохождения лучом 1 расстояния АА1 равно времени прохождения лучом 2 расстояния DC, поэтому

Δ=(A1 BC)n+λ/2=(A1 B1)n+λ/2=2dn cos r + λ/2

Таким образом, разность хода лучей 1 и 2 равна

                                    Δ=2dn cos r + λ/2              (10)   

Соответственно, при Δ=mλ    m=0,1,2,3,… наблюдается максимум интерференции, если же . Δ=(m+1/2),  m=0,1,2,… – минимум. 

Локализация интерференционных полос. Полосы равного наклона и равной толщины.

Из формулы (10) видно, что разность хода зависит как от толщины пластинки, так и от угла наклона лучей.

Чтобы наблюдать интерференционные полосы, отраженные лучи с помощью линзы собирают на экране (линзой может служить и хрусталик глаза, тогда экраном служит сетчатка, и мы наблюдаем картинку визуально)

Поставим экран в фокальной плоскости линзы (рис 5). Тогда все

параллельные лучи соберутся в точку на экране, и каждой точке будет соответствовать свой угол падения лучей, а значит и своя разность хода. На экране мы увидим интерференционную картинку в виде колец. Это

 полосы равного наклона. Они локализованы в бесконечности. Если наблюдать пластинку глазом и в белом свете, пластинка кажется окрашенной в определенный цвет – тот цвет, для которого при данном угле падения максимум. Так как хрусталик мал, мы наблюдаем только лучи под одним углом. Если же наблюдать пластинку под разными углами, она окажется окрашенной в разные цвета, в зависимости от угла.

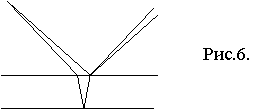Поставим экран так, чтобы на нем фокусировалась поверхность пластинки (Рис.6). Так как обычно источник света достаточно удален от пластинки, то для всех точек пластинки угол падения лучей примерно одинаков и разность хода зависит только от толщины пластинки в данном месте. Поэтому интерференционная картина  зависит от изменений толщины пластины. Так, если это клин, о мы увидим полосы. Это полосы равной толщины.

 

 

 

 

 

В обоих случаях можно пользоваться протяженным источником и белым светом (однако только если пластинка достаточно тонкая).

Минимальная толщина пластинки. При d=0 разность хода равна половине длины волны, и  это соответствует минимуму интенсивности. Пластинка кажется темной (поверхность мыльного пузыря перед тем, как пузырь лопнет, темнеет). Максимуму  (первому) соответствует толщина 2dn=λ/2 откуда минимальная толщина пластинки (пленки) равна d=λ/(4n), пленка может быть даже тоньше длины волны.

 

Кольца Ньютона.

Линза лежит на плоской поверхности (рис.7). Между нижней поверхности линзы и поверхностью пластинки образуется воздушный зазор, интерферируют лучи, отраженные от этих поверхностей. Это частный случай полос  равной толщины. Интерференционная картинка имеет вид колец. Рассчитаем разность хода лучей, отраженных от поверхности пластинки (плоской) и сферической поверхности положенной на нее линзы. Δ=2t+λ/2.  Условия образования темных колец Δ=2t+λ/2=mλ+λ/2  (будем ориентироваться на темные,  а не на светлые кольца, чтобы избежать неудобного слагаемого λ/2). Определяем толщину воздушного промежутка  t между поверхностями

Здесь ρ – радиус темного кольца. Так как t<<R , то членом   можно пренебречь, и тогда получим 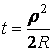., откуда

В центре – темное пятно.(За счет потери полуволны при отражении от очень тонкой прослойки. Или, если эта прослойка практически бесконечно тонкая- сравнима с межатомными расстояниями, то получается «оптический контакт» –отражения нет, так как нет границы между двумя поверхностями.

  Если рассматривать картинку «на просвет»  – темные и светлые кольца меняются местами.